Objeto de estudo da Física, mais especificamente da Mecânica Clássica, a Resistência dos Materiais (RESMAT) fundamenta-se compulsoriamente na compreensão da Lei de Hooke, que foi elaborada em 1676 e publicada somente dois anos mais tarde, em Londres pelo cientista Inglês Robert Hooke, que descreveu os pormenores do comportamento de deformação elástica e plástica dos materiais em função da tensão perpendicular aplicada a eles, através de um simples ensaio de tração com molas, registrado no livro Lectures de Potentia Restitutiva, or of spring explaining the power of springing bodies, que em português significa Aulas de Tensão Restauradora, ou da mola demonstrando o poder de elasticidade dos corpos.
Há cerca de dois anos, publiquei esta teoria em um anagrama “ceiiinosssttuv” no final do livro intitulado como “A verdadeira teoria da elasticidade”, para omitir a frase latina “Ut tensio sic vis” que significa: A deformação é proporcional à tensão aplicada.
Robert Hook, 1678
1 - Revisão da literatura
Apesar do embate epistolar protagonizado pelos cientistas Robert Hooke e Isaac Newton, e das diversas e controversas interpretações e opiniões acerca da relação hostil entre eles, é consenso na comunidade científica que ambos contribuíram de forma imensurável para a Revolução Científica, o que nos obriga a desprezar as polêmicas e considerar apenas as contribuíções que esses gigantes fizeram para a Mecânica Clássica, pois independentemente da estatura e do reconhecimento conquistado, a capacidade cognitiva deles foi determinante na concepção dos fundamentos da Física, uma vez que ambos pertenceram à Royal Society, entidade onde as mentes mais brilhantes reuniam-se para a prática da ciência experimental, que possibilitou o acúmulo de conhecimento necessário para alavancar a Revolução Industrial.
Contudo é necessário considerar que na revisão bibliográfica deste artigo as Leis de Newton são descritas e mencionadas de forma anacrônica, ou seja, antes da Lei de Hooke, apenas por questões didáticas, e que cronologicamente elas foram publicadas aproximadamente dez (10) anos após a publicação da Lei de Hooke, o que por si só evidencia que Robert Hooke conhecia previamente, pelo menos de forma empírica, as Leis que renderam a Isaac Newton a consagração como o cientista mais importante de sua época, fato este que sugere a possibilidade de plágio e gera muita polêmica entre cientistas, pesquisadores e historiadores que em alguns casos sugerem até mesmo a possibilidade de revisionismo histórico, com o objetivo de ajustar os ponteiros deste embate de titãs.
1.1 - Dinâmica
Em 1687, Isaac Newton consagrou-se como o cientista mais importante de sua época, com a publicação do livro Philosophiae Naturalis Principia Mathematica, que em português significa Os Princípios Matemáticos da Filosofia Natural, onde enunciou os fundamentos da Dinâmica, que é o ramo da Mecânica Clássica que e estuda o movimento, ou seja, a variação da posição de um objeto ou ponto material no espaço em função do tempo, assim como suas causas.
1.2 - Movimento
O Movimento de um corpo é a variação, em relação a um determinado referencial, da posição de um objeto ou ponto material em função do espaço.
1.3 - Velocidade
A Velocidade de um corpo é a variação, em relação a um determinado referencial, da posição de um objeto ou ponto material em função do espaço e do tempo.
1.4 - Força
Em sua obra prima, Isaac Newton atribuiu a causa do movimento de um corpo à relação de forças a que ele é submetido, conforme pormenorizado na Primeira Lei de Newton que diz:
Se nenhuma força resultante atua sobre um corpo (F = 0), a velocidade não pode mudar, ou seja, o corpo não pode sofrer uma aceleração.
Isaac Newton, 1687
Portanto:
\[\overrightarrow{F}=\sum_{i=1}^nF_{l}=\overrightarrow{F}_{1}+\overrightarrow{F}_{2}+...+\overrightarrow{F}_{n}\] |
Equação 01 |
Quando a Força Resultante exercida em um corpo é diferente de zero, obtém-se a condição necessária para que ele adquira aceleração e velocidade, o que faz com que ele se movimente em relação ao espaço, conforme pormenorizado na Segunda Lei de Newton que diz:
A força resultante que age sobre um corpo é igual ao produto da massa do corpo pela aceleração.
Isaac Newton, 1687
Portanto:
\[F=m.a\] |
Equação 02 |
1.4.1 - Tipos de Forças
- Força Gravitacional (G)
- Força Peso (P)
- Força Elástica (Fel)
- Força Centrípeta (Fcp)
- Força Magnética (Fm)
- Força de Atrito (Fat)
- Força Normal (N)
Obs.: Destacadas em negrito as forças cuja compreensão é pré-requisito para a plena interpretação e assimilação da Lei de Hooke.
1.5 - Aceleração
A Aceleração de um corpo é a grandeza utilizada para mensurar a variação de velocidade de um corpo ou ponto material em função do tempo, conforme pormenorizado na Segunda Lei de Newton que diz:
A força resultante que age sobre um corpo é igual ao produto da massa do corpo pela aceleração.
Isaac Newton, 1687
Ou seja:
\[F=m.a\] |
Equação 02 |
Portanto:
\[a=\frac{F}{m}\] |
Equação 03 |
1.6 - Aceleração da Gravidade (g)
Um corpo em queda livre na atmosfera terrestre, fica submetido a uma aceleração correspondente ao módulo da força gravitacional, conforme pormenorizado na Terceira Lei de Newton que diz:
Quando dois corpos interagem, as forças que cada corpo exerce sobre o outro são iguais em módulo e têm sentidos opostos.
Isaac Newton, 1687
Quando dois corpos se aproximam, surgem Forças com mesma intensidade e sentidos opostos →← que fazem com que os corpos se atraiam, ou seja, massa atraí massa.
\[g=9,80665 [m/s_{2}]\] |
Equação 04 |
Obs.: Para fins didáticos convencionou-se utilizar g=10m/s2
1.7 - Força Peso (P)
O Peso (P) de um corpo é o módulo da força necessária para impedir que o corpo caia livremente, medida em relação ao solo.
Halliday, et al, 2012
Em outras palavras, a Força Peso (P) é o módulo da Força Normal (N) necessária para manter um objeto em repouso suspenso por uma mola, capaz de anular a Aceleração da Gravidade (g) que a terra exerce sobre ele empurrando-o para baixo, ou seja, trata-se da Força Resultante (Fres) do produto da massa (m) do objeto pela Aceleração (a), que pode ser representada de forma equivalente a equação (02), substituindo apenas (F) por (P), da seguinte maneira:
\[P=m.a\] |
Equação 05 |
Sendo que neste caso a Aceleração (a) por se tratar de um movimento causado por um força conhecida, a Força Gravitacional (G), que ocorre na direção vertical e no sentido superior/inferior da superfície de um determinado planeta, deve ser substituída pelo módulo da Aceleração da Gravidade (g) específico deste planeta, conforme equação (06), ou seja, substituindo (a) por (g), da seguinte maneira:
\[P=m.g\] |
Equação 06 |
1.8 - Tensão
Quando uma mola é utilizada para suspender um determinado objeto e não é capaz de anular completamente o Peso (P) dele, ela fica submetida a ação de uma força mecânica interna classificada como tensão de tração, ou somente Tensão (σ), que pode ocorrer tanto na seção longitudinal σAl como na transversal σCo do material que a constitui e causar Deformações (x) de alongamento xAl e contração xCo respectivamente, enquanto não ultrapassa o limite de elasticidade, pois a partir dele ocorre a deformação plástica, até o limite de ruptura, onde o material sofre uma fratura.
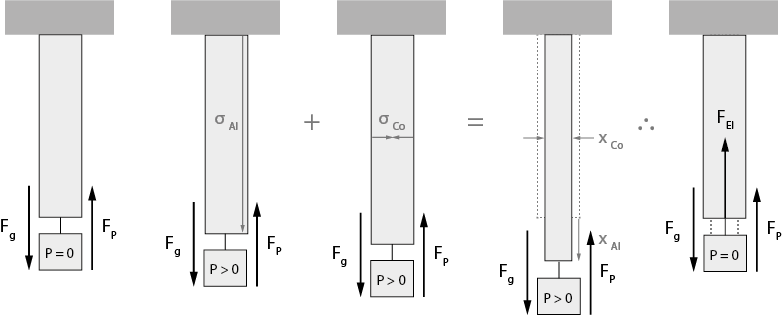 Figura 1 - Relação entre a Força Gravitacional e a Força Peso.
Figura 1 - Relação entre a Força Gravitacional e a Força Peso.
1.9 - Lei de Hooke
Um material tem comportamento elástico quando as deformações causadas por determinada tensão desaparecem com a retirada dela. Chama-se limite de elasticidade do material o maior valor de tensão para o qual o material ainda apresenta comportamento elástico. (BEER, et al., 1995).
 Figura 2 - Curva tensão x deformação e limite de elasticidade (a).
Figura 2 - Curva tensão x deformação e limite de elasticidade (a).
Para a maioria dos materiais que são submetidos a uma tensão de tração em níveis relativamente baixos, a tensão e a deformação são proporcionais entre sí. (HOOKE, 1678).
A intensidade da Tensão (P), é proporcional a Deformação Elástica (x) e inversamente proporcional a Força Elástica (Fel), até o limite de elasticidade específico do material e Robert Hooke provou isso ao determinar a Constante Elástica (k) de uma mola, que é uma característica intrinseca a composição e as dimensões do material que a constitui, através de um experimento em laboratório equivalente ao reproduzido a seguir:
Lei de Hooke:
\[F_{el}=k\ .\ x\] |
Equação 07 |
Matematicamente:
\[k=\frac{P}{x}\] |
Equação 08 |
Vetorialmente:
\[F_{el}=-k\ .\ x\] |
Equação 09 |
O sinal negativo (-) na equação vetorial indica que a força elástica e a deformação são representadas por vetores com sentidos opostos
Considerando que:
\[x=\triangle L\] |
Equação 10 |
então:
\[x = L - L_{0}\] |
Equação 11 |
Fel = Força Elástica mensurada em [N]
k = Constante Elástica mensurada em [N/m]
x = Deformação Elástica mensurada em [m]
L = Comprimento mensurado em [m]
FP = Tensão causadora da deformação mensurada em [N]
m = Massa [Kg]
Fa = Aceleração [m/s²]
Fg = Força Gravitacional [m/s²]
2 - Ensaio experimental
Através deste um ensaio realizado em laboratório e da observação dos fenômenos físicos e químicos, relacionados com o comportamento tensão-deformação de uma mola submetida a uma Tensão (P), foi possível determinar matematicamente os efeitos de Deformação Elástica (x) (não definitiva), assim como a Constante Elástica (k) do material e a Força Elástica (Fel) gerada em função da tensão apliacada na mola.
Os recursos necessários para reproduzir o ensaio e observar os fenômenos a serem estudados foram: Um dinamômetro, um suporte para suspendê-lo, discos de metal com massas conhecidas e diferentes, um suporte para alojar os discos, uma régua milimétrica e uma mola.
O dispositivo foi montado a partir de um suporte capaz de fixar na posição vertical o dinamômetro, que por sua vez suspendeu a mola, que recebeu em sua extremidade inferior um suporte para alojar os discos de metal.
Durante o experimento ficou evidente, a existência de uma força contrária à exercida pelos discos sobre a mola. Sendo que, essa força contrária foi responsável por desfazer a deformação elástica que a mola sofreu, e por restaurar as suas características originais.
A tensão elástica é capaz de devolver à mola as suas características originais, após uma deformação elástica e é aplicável também a outros tipos de materiais além do metal, como por exemplo, madeira, pedra, terra, cabelos, chifres, ossos, seda, tendões, vidro e similares (HOOKE, 1678).
Essa força restauradora analisada tem origem intermolecular e é proveniente das propriedades químicas que mantém as moléculas e átomos unidos.
“Em uma escala atômica, a deformação elástica macroscópica é manifestada na forma de pequenas alterações no espaçamento interatômico e na extensão das ligações interatômicas” (CALLISTER, et al., 2006).
Após coletar todas as informações necessárias, através do ensaio descrito, foi necessário determinar a constante elástica da mola, sendo que para isso foi fundamental compreender o conceito da Lei de Hooke, e seu equacionamento matemático, através da equação (08).
3 - Arranjo
Com o dispositivo montado, inicia-se o experimento, ao fixar o suporte para alojar os discos na extremidade inferior da mola, sem se esquecer de zerar a régua de forma a desprezar a massa do dispositivo.
4 - Procedimento experimental
Os discos de metal foram adicionados ao dispositivo um a um, gradativamente, enquanto se era feito o registro da deformação da mola mensurada a cada alteração.
5 - Características e incertezas
Cabe destacar a necessidade de considerar que de acordo com os fundamentos físicos, descritos pela termodinâmica, que estuda causas e os efeitos de mudanças na temperatura, pressão e volume, que mediante variação térmica a constante elástica deve manter-se a mesma, pois a medida inicial da mola sofre dilatação térmica proporcional a dilatação total da mola.
Se a temperatura de uma barra metálica de comprimento L aumenta de um valor ∆t, seu comprimento aumenta de um valor ∆L=Lα.∆T onde α é uma constante chamada coeficiente de dilatação linear. Se a temperatura de uma barra metálica de comprimento L aumenta de um valor ∆t, seu comprimento aumenta de um valor ∆L=Lα.∆T onde α é uma constante chamada coeficiente de dilatação linear” (HALLIDAY, et al., 2012).
Durante o experimento, foi necessário observar três incertezas relevantes que poderiam influenciar e induzir o resultado do ensaio ao erro, sendo elas:
- Incerteza humana: Ocasionada por um erro humano que pode ocorrer durante a coleta de informações, ao mensurar as deformações da mola.
- Incerteza física: Ocasionada por um erro natural que pode ocorrer devido à fadiga do material que compõe a mola, por rompimento do material.
- Incerteza mecânica: Ocasionada por um erro no ajuste ou posicionamento do dispositivo utilizado no ensaio.
6 - Cuidados particulares e relevantes
Durante o experimento, alguns detalhes foram cuidadosamente observados, para não influenciar no resultado final, pois foram fundamentais para evitar que a mola sofresse uma possível deformação plástica:
- Não esticar a mola demasiadamente;
- Colocar as massas, segurando o suporte e soltando lentamente;
- Distribuir uniformemente as massas, para evitar a queda.
7 - Aplicações e curiosidades
A Lei de Hooke é utilizada pela Engenharia Civil como parte do cálculo estrutural nos projetos de edificações como residências, edifícios, estradas e pontes, pela Engenharia Mecânica como parte do cálculo de precisão do projeto de aviões, aeronaves, navios, pontes, veículos, trilhos, máquinas e relógios, além de ser utilizada amplamente nas Engenharias Elétrica e Eletrônica, que a utilizam como parte do cálculo do projeto de balanças, células de cargas, torquimetros, dinamômetros, transdutores e sensores, além de ampla utilização do conceito na extensometria, que é uma técnica que permite mensurar tensões e deformações dos materiais, que integra todas as Engenharias.
8 - Obtenção de dados em laboratório
Para calcular a constante elástica da mola, foi necessário obter dados acerca da deformação elástica do material através da equação (11), utilizada para mensurar a deformação sofrida por ele, de acordo com a variação de tensão gerada ao acrescentar os discos de metal ao suporte, portanto os dados obtidos em laboratório foram:
| Peso x Deformação | ∆x1 | ∆x2 | ∆x3 | ∆x4 | ∆x5 | ∆x6 |
| Peso [N] = m[kg].10 (g) | 50 | 100 | 150 | 200 | 250 | 300 |
| Deformação [m] . 10-3 (mm) | 10 | 20 | 30 | 40 | 50 | 60 |
9 - Conversão dos dados da tensão
Após obter e registrar os dados acerca da deformação elástica sofrida pela mola, foi necessário aplicá-los na equação (08) para obter o valor da constante elástica, porém, antes disso foi necessário realizar uma série de conversões de unidades, para nivelar os dados obtidos, com os solicitados pelas equações que constituem a famigerada Lei de Hooke, cujas unidades de medidas são representadas de acordo com o Sistema Internacional (SI) de medidas.
Para obter a medida do Peso [N] a massa [g] obtida em laboratório foi convertida em massa [kg] conforme equação (04):
\[m [kg]=\color{red} {m[g]}.10^{-3}\] |
Equação 12 |
Portanto:
Em seguida foi necessário aplicar a equação (05) para transformar as medidas obtidas em Peso [N]:
\[P=m.a\] |
Equação 05 |
P = Peso
m = massa
a = aceleração
Sendo que a variável “a” por se tratar de uma aceleração vertical, causada pela lei da gravidade, pode ser substituída por “g” que é a aceleração da gravidade, ou seja, 10 [m/s2], através da equação (06).
\[P=m.g\] |
Equação 06 |
ou:
\[P[N]=m[kg].10[m/s^2]\] |
Equação 13 |
Portanto:
10 - Conversão dos dados da deformação
Para obter a medida da Deformação [m] a Deformação [mm] deve ser convertida conforme equação (14):
\[D[m]=\color{blue} {D[mm]}.10^{-3}\] |
Equação 14 |
Portanto:
11 - Organização dos dados de tensão e deformação
| Dados obtidos durante o experimento |
Dados convertidos para o SI (Sistema Internacional) |
||||
| Massa [g] |
Massa [kg] |
Deformação [mm] |
Peso [N] |
Deformação [m] |
|
| ∆x1 | 50 | 0,05 | 10 | 0,5 | 0,01 |
| ∆x2 | 100 | 0,10 | 20 | 1,0 | 0,02 |
| ∆x3 | 150 | 0,15 | 30 | 1,5 | 0,03 |
| ∆x4 | 200 | 0,20 | 40 | 2,0 | 0,04 |
| ∆x5 | 250 | 0,25 | 50 | 2,5 | 0,05 |
| ∆x6 | 300 | 0,30 | 60 | 3,0 | 0,06 |
12 - Modelagem matemática
Enfim, após determinar as medidas P[N] e Deformação [m], os dados obtidos foram inseridos na equação (8) para determinar a constante elástica (k) da mola, conforme descrito a seguir:
∆x1 equivale ao peso de 0,5 [N] e a uma deformação de 0,01 [m], ou seja:
∆x2 equivale ao peso de 1,0 [N] e a uma deformação de 0,02 [m], ou seja:
∆x3 equivale ao peso de 1,5 [N] e a uma deformação de 0,03 [m], ou seja:
∆x4 equivale ao peso de 2,0 [N] e a uma deformação de 0,04 [m], ou seja:
∆x5 equivale ao peso de 2,5 [N] e a uma deformação de 0,05 [m], ou seja:
∆x6 equivale ao peso de 3,0 [N] e a uma deformação de 0,06 [m], ou seja:
| Peso [N] |
Deformação [m] |
k = P/∆x [N/m] |
|
| ∆x1 | 0,5 | 0,01 | 50 |
| ∆x2 | 1,0 | 0,02 | 50 |
| ∆x3 | 1,5 | 0,03 | 50 |
| ∆x4 | 2,0 | 0,04 | 50 |
| ∆x5 | 2,5 | 0,05 | 50 |
| ∆x6 | 3,0 | 0,06 | 50 |
Desta forma com auxílio do conceito de análise dimensional, é irrefutável que se os dados obtidos de Deformação [mm] e da Constante Elástica (k) [N/m] forem aplicados na equação (3) que é a inversa da lei geral da elasticidade dos materiais, descrita por Robert Hooke, obtém-se um valor equivalente ao da medida Peso [N], porém, com sinal negativo, pois Fel nada mais é do que a tensão restauradora, responsável por devolver à mola suas características originais, fazendo-a repousar no seu estado inercial, observado no início do ensaio, ou seja, antes de submetê-la a tensão dos discos que causaram a deformação elástica no material.
| Peso [N] |
Deformação [m] |
k = P/∆x [N/m] |
Fel [N] |
|
| ∆x1 | 0,5 | 0,01 | 50 | -0,5 |
| ∆x2 | 1,0 | 0,02 | 50 | -1,0 |
| ∆x3 | 1,5 | 0,03 | 50 | -1,5 |
| ∆x4 | 2,0 | 0,04 | 50 | -2,0 |
| ∆x5 | 2,5 | 0,05 | 50 | -2,5 |
| ∆x6 | 3,0 | 0,06 | 50 | -3,0 |
Interpretação para ∆x1 : Quando a tensão vertical Peso [N] de 0,5 [N] foi aplicada na mola, a Deformação [m] mensurada foi de 0,01 [m], devido a Constante Elástica [k] de 50 [N/m] que é uma característica inerente ao material que constitui a mola, responsável por gerar uma tensão elástica Fel [N] na direção oposta de -0,5 [N].
Portanto conforme descrito por Robert Hooke e evidenciado neste ensaio, Fel [N] possui o mesmo valor vetorial que o Peso [N], ou seja: Os dois valores são medidas de forças inversamente proporcionais.
13 - Método gráfico dos mínimos quadrados
Utilizando o método gráfico e dos mínimos quadrados, a constante elástica k pode ser representada através de uma razão trigonométrica, conforme Figura 2:
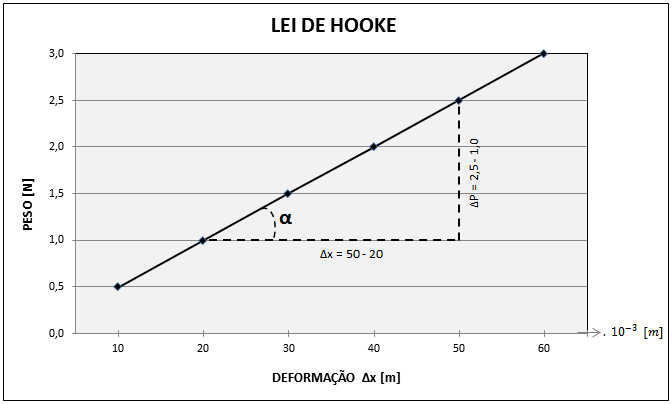
Figura 2 - Mínimos quadrados da lei de Hooke.
\[k=tg\ \alpha = \frac{\triangle P}{\triangle x}\] |
Equação 15 |
Então:
Portanto:
14 - Análise dos resultados
O valor da constante elástica pode ser obtido de duas maneiras diferentes, através do equacionamento (Lei de Hooke) e da representação gráfica (Método dos mínimos quadrados), porém no segundo caso é necessário enfatizar que a constante elástica deve ser definida pela média entre os pontos gerados no gráfico, isso se faz necessário para corrigir uma eventual anamorfose que pode fazer com que os pontos fiquem desalinhados, portanto, na representação gráfica essa média permite traçar uma reta, que expressa à deformação ∆x em função do Peso [P] de forma fidedigna.
15 - Conclusões do ensaio
Através do experimento conclui-se que a tensão restauradora produzida pela mola depende da da composição química, da espessura, do fio de enrolamento e do número e diâmetro de espirais que a constituí, ou seja, varia de acordo com a concentração de massa dela, pois tal força tem síntese intermolecular e origina-se da força que mantém as moléculas e os átomos unidos, além do que é inversamente proporcional a tensão aplicada sobre o material respeitando o limite elástico dele, pois ao ultrapassar esse limite tal força provoca uma deformação plástica na mola, impossibilitando que ela volte ao seu estado original, ou seja, ao seu estado de inércia.
Sendo a constante elástica dependente da composição química do material que compõe a mola, conclui-se que cada mola possui um valor diferente para k, pois dificilmente duas molas terão a mesma concentração de massa.
A força observada foi simplesmente o produto da constante pela medida da deformação elástica, e a constante igual à divisão do peso que gerou a deformação pela medida da deformação da mola durante o ensaio.
Portanto conclui-se que a deformação elástica dos materiais, pode ser utilizada de forma eficaz, como fonte geradora de sinal de variação, para medição de grandezas físicas relacionadas, por exemplo, as forças de aceleração e torque, ou seja na extensometria.
16 - Referências Bibliográficas
HALLIDAY David, RESNICK Robert e WALKER Jearl Fundamentos da Física, Volume I [Livro]. - Rio de Janeiro: LTC, 2012.
CALLISTER Jr. e D. WILLIAM. Fundamentos da Ciência e Engenharia de Materiais. 2. ed. [Livro]. - Rio de Janeiro: LTC, 2006.
BEER F.P. e JOHNSTON Jr. E.R. Resistência dos Materiais. 3. ed [Livro]. - São Paulo: Pearson Makron Books, 1995.
NEWTON Isaac. Philosophiae Naturalis Principia Mathematica. [Livro]. - London: John Machin, 1687, minha tradução.
HOOKE Robert. Lectures de Potentia Restitutiva, or of springexplaining the power of springing bodies. [Livro]. - London: John Martin, 1678, minha tradução.










