O MTBF, seu significado e suas limitações para uso como parâmetro de Confiabilidade e para fins de Planejamento de Manutenção. “Uma medida básica de confiabilidade para itens reparáveis: o número médio de vida de unidades durante as quais todas as partes do item operam dentro de seus respectivos limites, durante um intervalo particular de medição sob condições específicas” (Este padrão deixou de ter validade em 1995). Indicador de Manutenção: Como calcular MTBF?
O QUE SIGNIFICA E SUAS LIMITAÇÕES
I. Definição:
Em 1981, o padrão militar MIL-STD-721C – Definition of Terms for Reliability and Maintainability definiu o MTBF (Mean Time Between Failures) dessa forma:
“Uma medida básica de confiabilidade para itens reparáveis: o número médio de vida de unidades durante as quais todas as partes do item operam dentro de seus respectivos limites, durante um intervalo particular de medição sob condições específicas” (Este padrão deixou de ter validade em 1995).
II. Premissas de Validade:
- Válido para itens reparáveis
- O tempo de parada para reparo deve ser insignificante em relação ao tempo total do ensaio (tempo considerado para o cálculo)
- O item após o reparo deve ser considerado tão bom quanto novo (As Good As New)
- A taxa de falha do item em análise deve ser constante
III. Fórmula para o cálculo do MTBF:
É muito simples calcular o MTBF porque trata-se de uma simples média aritmética. Esta é a razão pela qual tanta gente usa o MTBF como indicador de Confiabilidade ou para efeitos de planejamento, porém, como diz a premissa 4, a taxa de falha do item em análise deve ser constante e isso é assumido cotidianamente sem uma análise mais profunda dos dados de falha.
onde
é o tempo de ensaio, ou tempo de observação
R é a quantidade de falhas durante o
Nota: Item pode significar equipamento, equipamento secundário, item manutenível ou peça (não manutenível). Quando tratamos de item não manutenível (peça), calculamos o MTTF (Mean Time to Fail).
Ex.: Se o período escolhido para determinação do MTBF de um determinado item manutenível é de 1 ano e este item trabalha 12 horas/dia, 5 dias por semana e em média 4 semanas/mês, em um ano o tempo médio de ensaio seria:
Ou seja, 2880 horas são as horas que o item trabalhou, subtraindo-se fins de semana, feriados e manutenções planejadas. Vamos imaginar que o item em análise teve 5 falhas neste período. Qual é o MTBF?
Agora vamos supor que cada quebra representou 8 horas de parada do equipamento para reparo. Portanto, um total de 40 horas de “downtime”.
Em que isto afeta o cálculo do MTBF? Se eu descontar esse tempo de parada do tempo total de ensaio, como fica o novo MTBF?
Esse valor é apenas 1,4% menor. Considerando-se todas as premissas para o cálculo do MTBF, principalmente a restrição da taxa de falha constante, essa diferença não significa nada. Se o downtime for muito grande, fere a 2ª premissa e o cálculo não vale.
IV. A Confiabilidade R(t) numa distribuição com taxa de falha constante
Quando dizemos que o MTBF é de 576 horas e isto é o mesmo que dizer que seu equipamento apresenta 1 falha a cada 576 horas em média, ou seja, o MTBF é, na verdade, o inverso da taxa de falha (λ).
\[MTBF=\frac{t_e}{R}=\frac{2880}{5}=\ 576\ horas\] |
\[λ=\frac{1}{MTBF}=\frac{1}{576}=\ 17x10^{-4}\ falha/hora\] |
O cálculo da Confiabilidade nos dará a probabilidade do item estar operando, sob condições específicas e para um determinado tempo. No caso da taxa de falha constante (λ):
Como admitimos taxa de falha constante, a Confiabilidade é a mesma para um mesmo tempo, desde que este esteja funcionando no momento do cálculo. Isto implica dizer que o equipamento não envelhece porque, se envelhecer, a taxa de falha muda, passa a não ser mais constante. Portanto é necessário conhecer bem como o cálculo do MTBF foi feito, principalmente o tempo considerado. Outro fato interessante é que, se calcularmos a Confiabilidade R(t) para um tempo igual ao MTBF, o valor será 36,8%, ou seja, a probabilidade que o equipamento tenha falhado até aquele tempo é de 63,2%. Isto acontece porque a Confiabilidade decresce exponencialmente com o tempo, conforme ilustra o gráfico abaixo.
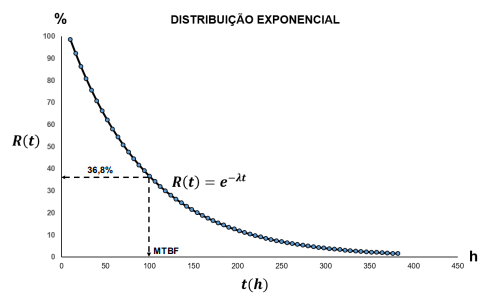
Para cada valor de “t”, calcula-se a Confiabilidade. Vamos supor que se queira saber a probabilidade de o item estar funcionando depois de 1000 horas de operação.
Se passadas 1000 horas de operação, o equipamento estiver funcionando, ao se calcular uma nova Confiabilidade para as próximas 1000 horas, o valor será exatamente o mesmo, ou seja, 18,3 % porque a taxa de falha é admitida constante ao se calcular o MTBF.Diz-se que o item não envelhece nunca, o que é uma impossibilidade física.
Isto tudo nos leva às seguintes conclusões:
V. O que o MTBF É e o que o MTBF NÃO É:
Ref.: SCHENKELBERG, F – The Reliability Metric, R Publishing, 2015
Ele É:
O MTBF é o 63º percentil para a família de distribuições exponenciais. Outras distribuições podem resultar em MTBF em diferentes percentis da distribuição.
Ele NÃO É:
- Período livre de falhas
- O 50º percentil do tempo para falhar (a menos que o TTF* siga uma Normal)
- Aplicável em taxas de falhas decrescentes (falhas prematuras ou mortalidade infantil)
- Aplicável em taxas de falhas crescentes (fase de desgaste)
(*) Tempo para Falhar (Time To Fail)
VI. Cuidado ao usar o MTBF no Planejamento de Manutenção:
Como o cálculo do MTBF não se preocupa em como as falhas acontecem, ou seja, sua distribuição no tempo, um problema sério pode ocorrer. Veja no exemplo:
Ex.: Dois equipamentos iguais foram observados durante 10 mil horas para se determinar o MTBF de cada um. Nesse período, 5 falhas foram observadas e estão ilustradas abaixo. O cálculo do MTBF mostra valor idêntico para os dois equipamentos.
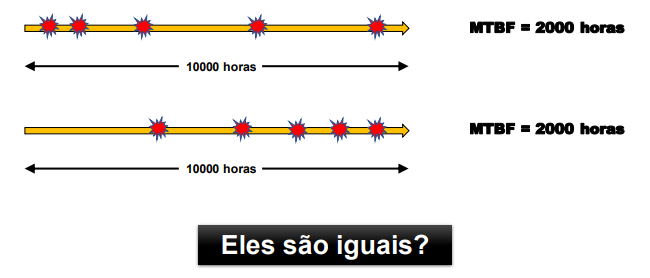
Evidentemente, o comportamento dos tempos para falhar são bem diferentes. Como usar o MTBF para planejar intervenções de manutenção proativa (Preventiva e Preditiva)? O segundo equipamento parece mostrar um comportamento de desgaste, ao passo que o primeiro tem falhas concentradas no início e depois parecem seguir uma taxa constante.
É muito difícil que as taxas de falha sejam constantes, portanto, sempre haverá erro ao se usar o MTBF como indicador de Confiabilidade ou como parâmetro para planejamento. É preciso conhecer como as falhas se distribuem no tempo.
A melhor maneira de se tratar os dados de falha é fazer a análise por modo de falha, não simplesmente a falha do item em si. Então determina-se as intervenções de acordo com o que indica a distribuição das falhas. O melhor nesses casos é usar uma distribuição de Weibull e obter os parâmetros de β e η para saber se as falhas analisadas indicam mortalidade infantil, falhas aleatórias com taxa constante comportamento de desgaste e a vida característica, ou seja, o ponto onde a probabilidade do item entrar em falha até aquele ponto (η) é de 63,2%. Quando a distribuição é exponencial (taxa de falha constante), η=MTBF.
Há que se começar a esquecer o MTBF e passar a calcular a Confiabilidade R(t) conforme a distribuição dos TTF (Tempo Para Falhar).









