Nas grandes cidades do Brasil, é comum vermos afixados nos postes, nos muros, cartazes apregoando “Trago seu amor de volta em 3 dias”. Não sei por que, mas o padrão habitual é de três dias... Os métodos preconizados são tarot, búzios, cartas, bola de cristal e similares.
Excluindo a questão dos métodos e do prazo de três dias, no ambiente industrial as dúvidas são similares:
- Quanto tempo este equipamento irá operar sem falhar?
- Qual será a duração dos reparos?
- Quais as consequências desta falha?
Não sendo reconhecidamente uma boa prática recorrer a videntes ou a outros recursos menos ortodoxos, como obter as respostas às perguntas da Produção? De onde o “Pai Mantenedor” irá buscar as respostas?
A resposta pode reviver alguns traumas da faculdade, mas o fato é que será a Estatística a nos dar as respostas. Não com precisão absoluta, é claro, as com uma precisão maior e melhor do que os três dias de retorno o amor perdido de sua vida.
Estatística é uma ferramenta muito poderosa, mas, como toda ferramenta, nós, principalmente os Mantenedores, sabemos que há ferramentas específicas para cada atividade, há cuidados no manuseio e precauções a serem tomadas.
E, certamente, Estatística é uma ciência complexa. Tanto que, como toda ciência que transcende nosso incipiente conhecimento, suscita algumas frases lapidares:
- “Sem dados você é apenas mais uma pessoa com uma opinião.” - William Deming
- “A pessoa que tem um pé no forno, e a cabeça no freezer, tem excelente temperatura média.” - atribuído a Delfim Neto
- “A Estatística é como o biquíni, mostra muito, mas esconde o essencial.” - atribuído a Mário Henrique Simonsen
- “Estatística é a arte de torturar os números até que eles confessem o que queremos.” - Anônimo
- “Alguns usam a Estatística como os bêbados usam os postes de iluminação: mais como apoio do que para iluminar.” - Andrew Lang, escritor escocês
Cuidados com as amostras
Além de frases pitorescas, existem muitas distorções com relação à Estatística. Para exemplificar, uma destas distorções, muito aplicável à época atual (sem NENHUM viés político), é a seguinte:
“Pesquisas eleitorais não valem nada. Eu nunca fui pesquisado, nem conheço quem tenha sido pesquisado.”
Certamente, a grande maioria da população nunca foi perguntada sobre suas tendências políticas, em quem irá votar. Somos mais de 150 milhões de eleitores, e as pesquisas são feitas com poucos milhares de pessoas, portanto certamente a maioria de nós nunca foi pesquisada em uma eleição.
Mas isto não invalida a pesquisa!
Ao fazer um exame de sangue, para contagem de glóbulos brancos, vermelhos, plaquetas, teor de colesterol, triglicerídeos, de todo nosso sangue, cerca de 5 litros, é retirado uma amostra usualmente de 5 mililitros, um milésimo da quantidade total.
O problema não é o TAMANHO da amostra, é a REPRESENTATIVIDADE da amostra.
Se eu lançar uma pesquisa em uma rede social perguntando “Você gosta de responder pesquisas na Internet?”, provavelmente eu terei uma maciça maioria de respostas SIM, as quais NÃO representam a realidade, pois apenas os que GOSTAM de responder pesquisas responderam. Aqueles que não gostam, sequer responderam, mas certamente existem muitos!
Nesta mesma linha, se uma pesquisa eleitoral indicar 25% de preferência pelo candidato X, realizada com 2 mil entrevistados, um fervoroso defensor deste candidato X, que tem um canal no Youtube, pode tentar contradizer este resultado, afirmando que entre os 75 mil seguidores de seu canal, 90% são favoráveis ao candidato X. Obviamente, trata-se de uma amostra viciada, tendenciosa, pois certamente a maioria dos seguidores deste canal compartilham das convicções políticas (ou futebolísticas, profissionais, filosóficas...) do criador deste conteúdo.
Fatos e dados, claro! Mas, com cuidado!
Fatos e dados são importantes, mas é preciso distinguir DADOS de INFORMAÇÃO.
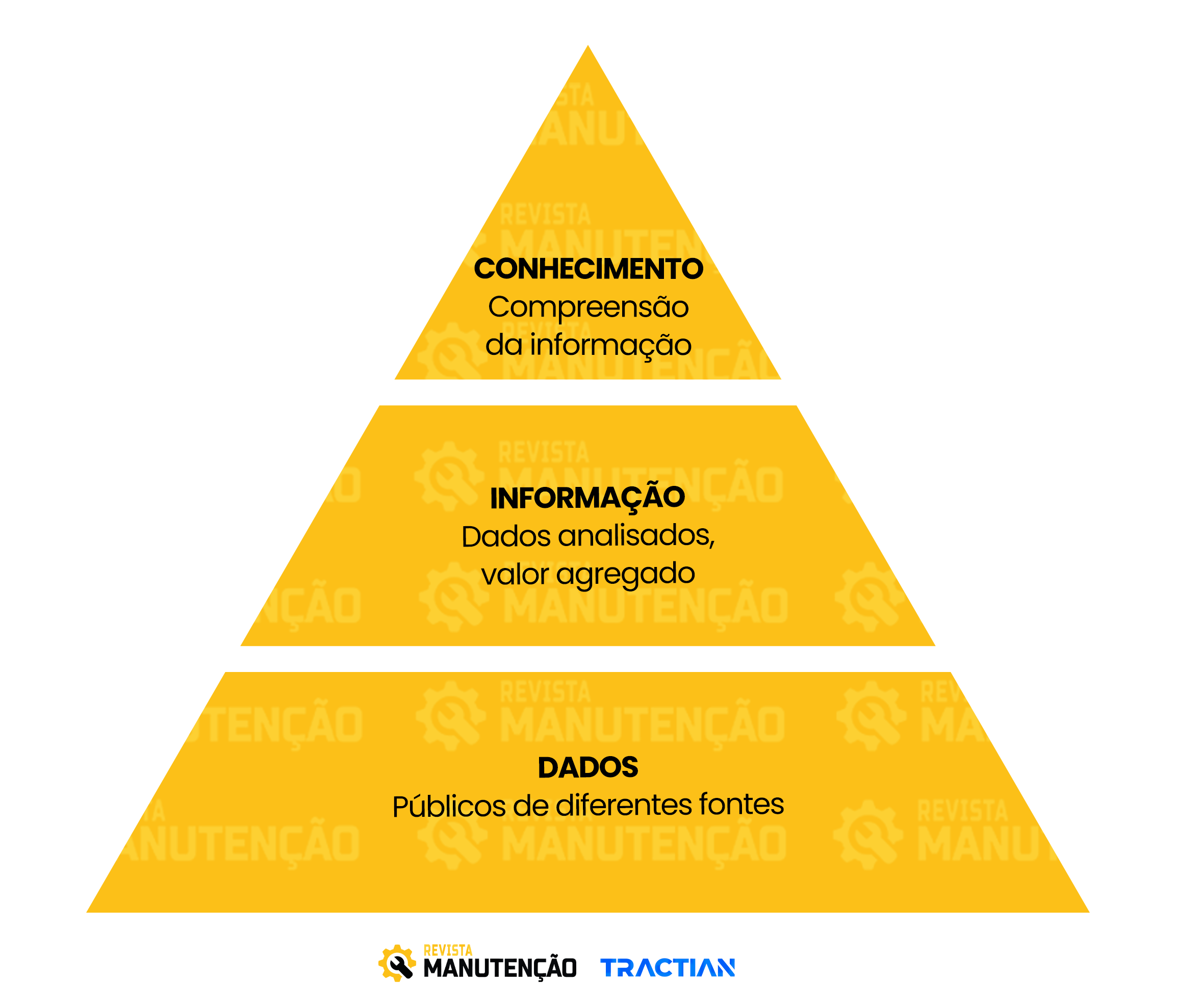
Dado é qualquer registro (físico ou mental) que pode ser associado a um objeto, pessoa ou evento.
O resultado do processamento de dados são as informações. As informações têm significado, podem ser tomadas decisões ou fazer afirmações considerando as informações.
Então, mais do que simplesmente basear nossas decisões, em Fatos e Dados, devemos apoiar nossas decisões em Informações.
Neste sentido, é muito esclarecedor a leitura (recomendo!) do livro “Factfulness: O hábito libertador de só ter opiniões baseadas em fatos” de Hans Rosling. Vou adaptar um exemplo deste livro para o Universo da Manutenção:
A empresa A conseguiu melhorar o MTBF (Mean Time Between Failures, em Português, TMEF, Tempo Médio Entre Falhas) em 40%! A empresa B melhorou seu MTBF em 15%.
Saiba as diferenças entre MTTR, MTBF e MTTF
Antes de, apressadamente, julgarmos qual empresa teve melhor desempenho, vamos checar algumas questões:
- Ao longo de quanto tempo? O período avaliado é o mesmo?
- Para qual equipamento? Estamos analisando o mesmo equipamento em ambas as empresas? As condições (operação, ambiente, etc.) em ambas as empresas é o mesmo.
- Ainda que as respostas às questões anteriores sejam afirmativas, a empresa A melhorou 40% sobre um MTBF de 150 dias. A empresa B melhorou 15% sobre um MTBF de 300 dias...
Estatística Descritiva e Inferencial
- A estatística descritiva é um ramo da estatística que aplica várias técnicas para descrever e sumarizar um conjunto de dados. Diferencia-se da estatística inferencial, ou estatística indutiva, pelo objetivo: organizar, sumarizar dados.
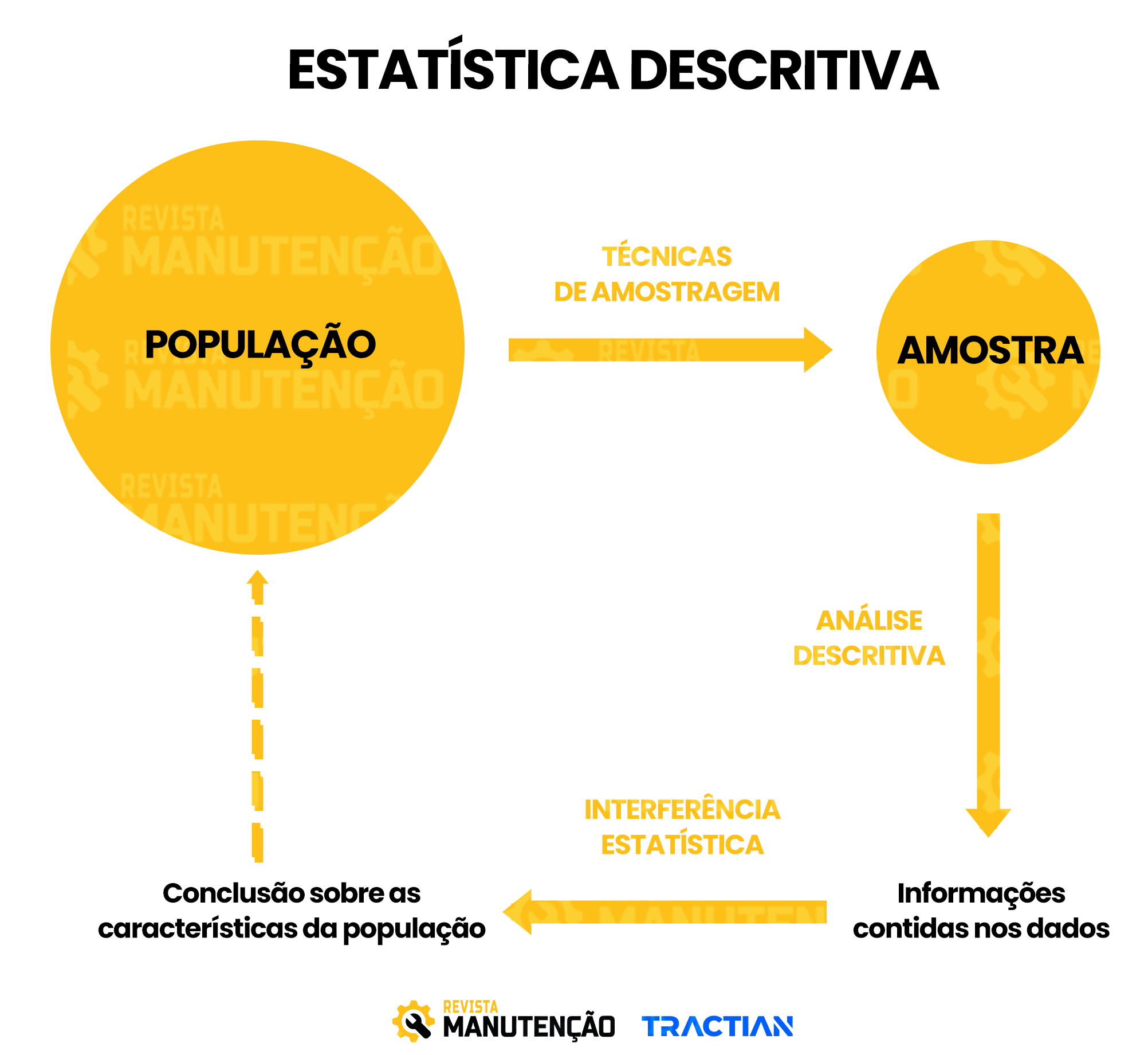
- Na estatística inferencial estamos sempre interessados em utilizar as informações de uma amostra para chegar a conclusões sobre um grupo maior, ao qual não temos acesso. Nesse sentido, uma ferramenta muito utilizada na estatística inferencial é a probabilidade.
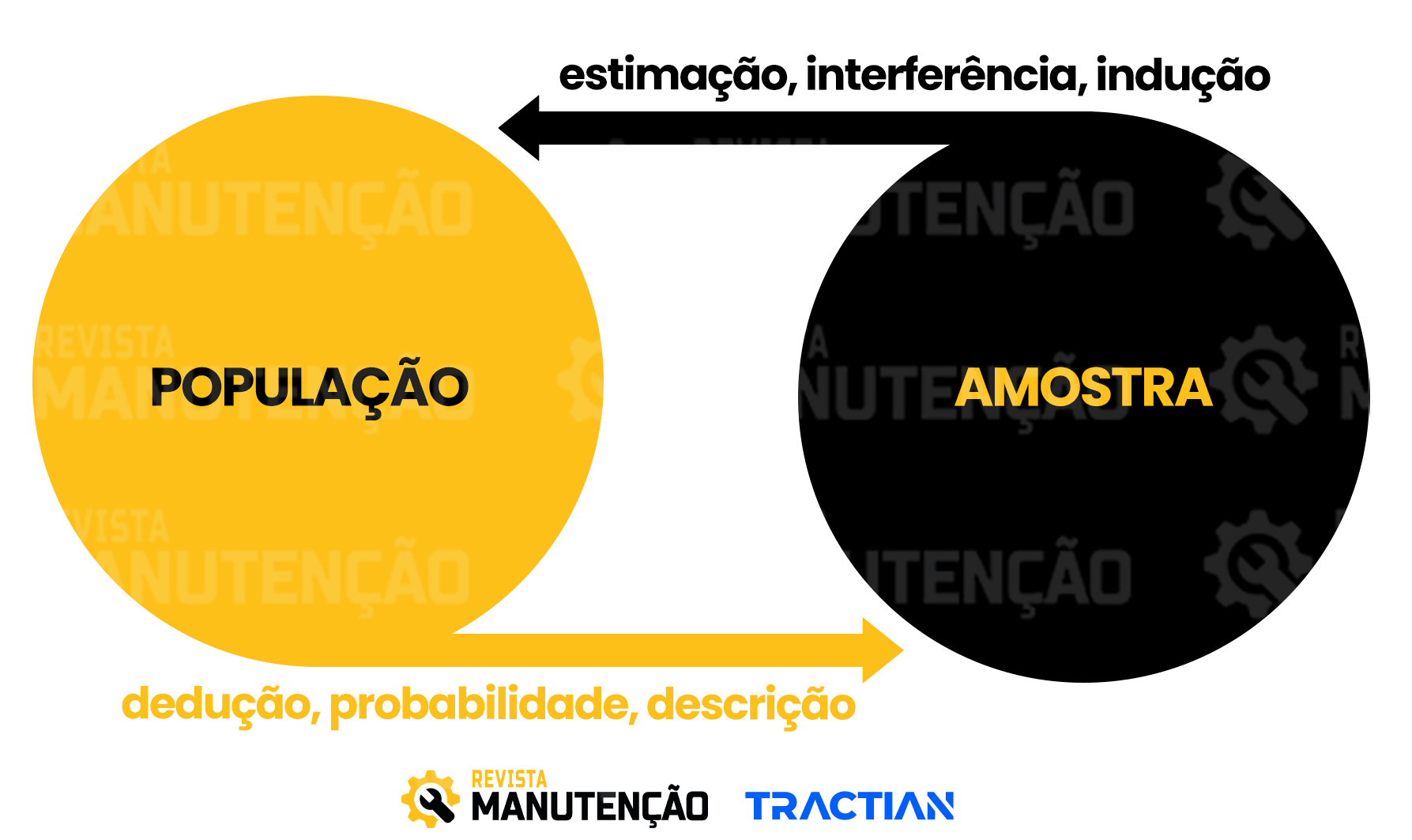
Obviamente, as previsões são obtidas através da Estatística Inferencial. Mas, para isto devemos trabalhar com dados, ou melhor, informações, obtidas através da Estatística Descritiva.
Neste sentido, John Moubray, principal desenvolvedor do conceito da Manutenção Centrada na Confiabilidade, enumerou alguns princípios nos quais descrevia a diferença entre a Visão Tradicional e a Visão da MCC. Um destes princípios citados por Moubray era:
Visão Tradicional: É necessário uma ampla base de dados para poder estabelecer um programa de manutenção bem sucedido.
Visão de Moubray: As decisões sobre a gestão de falhas de equipamentos terão de ser tomadas com base em dados incompletos e não abrangentes sobre taxas de falhas.
Por que desta visão de Moubray? Ele explica:
Dificuldades para obter um adequado banco de dados de manutenção:
- Tamanho da amostra: frequentemente, os processos industriais têm uma variedade muito grande de equipamentos, ou seja, há poucos equipamentos idênticos que possam gerar uma base de dados confiável. Ademais, a constante evolução dos equipamentos também faz com que os dados estejam em permanente mudança.
- Complexidade: a crescente complexidade dos equipamentos faz com que existam dezenas de modos de falha, dificultando a estratificação e a análise.
- Falhas: sendo a falha um não atendimento às funções do equipamento dentro do processo, como há os mesmos equipamentos trabalhando em diferentes unidades da planta, em condições distintas, gerando informações distintas e inconsistentes entre si.
- Paradoxo: mais se evitam falhas, menos informações terá sobre falhas! E basicamente, a função da Manutenção é evitar falhas, ou as consequências das falhas.
Principais ferramentas para a Gestão da Manutenção ter sucesso
Variáveis e Distribuições
Para poder avançar no entendimento e utilização da Estatística como ferramenta da Confiabilidade, é fundamental saber a distinção entre variáveis discretas e contínuas:
- Variável Discreta: Uma variável aleatória é discreta se o número de resultados possíveis é finito ou pode ser contado. Variáveis aleatórias discretas são determinadas por uma contagem.
Idades dos alunos em uma turma; quantidade de filhos homens em uma família com 4 filhos; número de bombas em manutenção ao longo de uma semana...
- Variável Contínua: Uma variável aleatória é contínua se pode assumir qualquer valor dentro de determinado intervalo. O número de resultados possíveis não pode ser listado.
Tempo que a pessoa leva de casa ao escritório; temperatura corporal ao longo de um período; tempo médio entre falhas de um determinado equipamento...
Além de conhecer os tipos de variáveis, é FUNDAMENTAL conhecer as várias possíveis distribuições probabilísticas:
Distribuição Binomial: a distribuição binomial tem as seguintes características:
- Espaço amostral finito;
- Apenas dois resultados possíveis (sucesso ou fracasso) para cada tentativa;
- Todos os elementos devem possuir possibilidades iguais de ocorrência;
- Eventos devem ser independentes uns dos outros.
Exemplos:
A probabilidade de filhos homens e mulheres em uma família: o número de filhos é finito (espaço amostral); dois resultados possíveis (menino ou menina), com a mesma probabilidade em cada novo nascimento (possibilidades iguais de ocorrência); o fato de ter tido 5 meninos, por exemplo, não afeta a probabilidade do sexo do sexto filho (eventos independentes).
Probabilidade de N defeitos em um lote de n componentes: N componentes, k defeitos (espaço amostral finito); dois resultados possíveis (defeituoso ou perfeito, ainda que não seja a mesma probabilidade, por exemplo 95% de probabilidade de ser perfeito, 5% com defeito); a probabilidade de defeito no décimo ou no vigésimo elemento do lote é a mesma (probabilidades iguais de ocorrência); o fato de um elemento ser defeituoso não impacta na probabilidade do elemento seguinte (eventos independentes).
Distribuição normal ou gaussiana: uma das mais importantes distribuições probabilísticas, mostra a distribuição de valores de uma variável contínua, em torno de um valor central. Tem aspecto de sino, e ilustra inúmeros fenômenos naturais, tais como distribuição da altura de pessoas da população: há um valor médio, e todas as medidas se distribuem em torno deste valor médio. Outras distribuições normais: peso dos recém-nascidos, pressão sanguínea da população...
Uma distribuição binomial, quando o número de eventos cresce indefinidamente, se aproxima da distribuição normal.
Para ficar perfeitamente caracterizada, basta conhecer a média e o desvio-padrão da distribuição normal.
Distribuição de Poisson: Distribuição discreta de probabilidade aplicável a ocorrências de um evento em um intervalo especificado. A distribuição binomial se refere ao número de sucessos em certo número de tentativas, enquanto a distribuição de Poisson se refere a um intervalo. Por exemplo:
- Número de falhas em um equipamento por mês
- Quantidade de bombas que falham em uma semana
- Número de equipamentos que chegam à oficina para manutenção por dia
Muito utilizada em teoria das filas, para dimensionar recursos requeridos em oficinas de manutenção para atender às necessidades, mantendo o backlog em níveis aceitáveis.
5 ferramentas fundamentais para análise de falhas
Distribuição Exponencial: enquanto a distribuição de Poisson avalia a quantidade de falhas por intervalo de tempo (por exemplo), – evento discreto - a distribuição exponencial avalia o intervalo de tempo para ocorrência da falha (evento contínuo). A distribuição exponencial é comumente usada para modelar probabilidades que vão decaindo com o tempo (assim como a probabilidade de um equipamento continuar funcionando). Por exemplo, conhecido o Tempo Médio Para Falhar (para equipamentos não reparáveis, tipo uma lâmpada), qual a probabilidade de este equipamento operar sem falhar durante um tempo t?
Distribuição de Weibull: nem sempre a distribuição da variável, por exemplo, intervalo entre falhas é tão bem “comportada” nos permita a utilização da distribuição exponencial. A distribuição de Weibull permite avaliar o comportamento estatístico de uma variável como falhas de equipamentos ou componentes, no período inicial da vida, normalmente denominado período de mortalidade infantil, como ao longo da vida útil propriamente dita e no período de desgaste. Uma das grandes vantagens da distribuição de Weibull é o fato de poder fazer previsões acuradas mesmo com pequeno número de dados, o que é, conforme destacou Moubray, uma característica cada vez mais presente na manutenção.
Então, a boa notícia é que temos várias ferramentas estatísticas, adequadas para inúmeras situações na gestão da manutenção e nos estudos de confiabilidade.
A má notícia é que não há videntes atuando no ramo... se você quer dominar a Engenharia de Confiabilidade, encare a fundo a Estatística!









